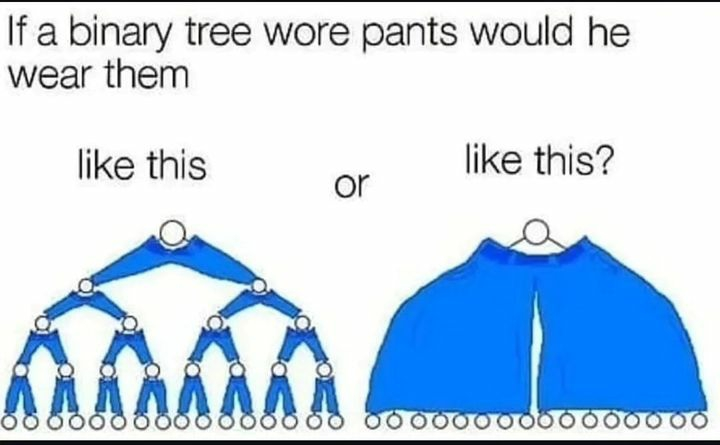
The one on the right, but each branch wears its own pants like a JNCO Matryoshka doll.
I was gonna argue for the left side as each child can be seen as the root of its own tree. But your logic is flawless, it's clearly the correct answer.
This is adorable and I love it
JNCOs are back in!
I've legit seen somebody wearing JNCOs within the last couple months. I think some people are trying to bring them back into style, and while I still won't wear them, I'd love to see them come back, anyway.
Honestly, I wanna see a lot of late 90s/early 00s fashion come back. I miss some of those looks.
Honestly, I wanna see a lot of late 90s/early 00s fashion come back. I miss some of those looks.
I miss wearing flannels. It might have been more early 90s, but I'm slow to pick up trends.
I don't think they are coming back for those of us who wore them originally but my 16 year old and lots of his friends freaking love them.
Just like the 60s came back in the 90s … the 90s are coming back in the 20s
Hint: it’s related to the old clothes people’s parents have in Their closets
I mean, clearly the underwear is worn like the left and the pants like the right.
Legit question: which requires the less amount of fabric?
Modeling a single pair of pants
For the sake of the calculation, lets model the pants as a prism, where:
- The top and Bottom surfaces are the front and back sides of the Pants with a surface of area A_t each.
- The Prism would have some depth that d depends on how thicc the binary tree is. For this calculation, I assume that d is constant for all pants
- The Pants have some outline that gives the circumference U of the prism
Total fabric for a given pair of pants p would then be A_p = A_tp * 2 + U_p * d
Nomenclature
Lets denote the two ways of wearing the pants as:
- W_1 | For a single pair of pants that covers the entire tree
- W_c | For many smaller pants that each cover a single node and its outgoing edges
First comparison
We can already note that the amount of fabric that is used, for the two possible ways to wear the pants, will depend on how densely the branches of the tree are packed. Assuming a maximally densely packed tree (if such is possible), where there is no space in between any branches, we'd get a the same area for A_t on the single pants for W_1 and the sum of all A_tp over all little pants in W_c:
A_tW1 = sum( A_tp ) for all pants p in W_c
It's clear then, that the area difference between W_1 and W_c then only depends on the circumference U_1 in W_1 VS the circumferences U_p in W_c. In this case, the sum of all U_p for each pair of pants p in W_c must be higher than U_1 in W_1, as long as the binary tree has a depth of at least two. This is because the pants would have to have to cover an exterior outline of at least U_1 and in addition there would interior borders between the pants.
Therefore, for a maximally packed tree, W_1 would use less fabric than W_c. On the other hand, given a tree where the siblings would be far away from each other, there would be a lot of space between the siblings. This would then diminish the areas A_tp for the pants in W_c in comparison to A_1 in W_1. (I know this isn't very rigorous here, but I don't want to go into too much depth here)
From this, we learn that the comparison of W_1 and W_c depends on the packing density of the pants.
Packing density
The packing density depends on the difference in branch length between children and parents within the tree. It also depends on the angle of the bottom branches to each other. For higher nodes, I'd assume that a node will always be horizontally aligned in the middle between it's child nodes. Therefore, the angle is only dependent on the length of the legs for non-bottom nodes.
I need to stop now as I'm hungry
Maybe I'll pick up where I left later.
This is so stupid but I love it
It needs a skirt.
I think I like the many individual pants the best ^^
the right pictures is the equivalent of 31 nodes in a trenchcoat to impersonate a root
yes, fellow root, indeed.
If that's a binary tree, what do non-binary trees look like?
Kinda like this:

Each knot has two smaller and one bigger child knot? That's queer
Each branch has however many children, of whichever size, as is required by the application
Splay tree gets tangled up pulling a leg out and falls down the stairs
Yes or no, we need the answer!
Whose binary tree? Mine have more than two legs
Memes
Post memes here.
A meme is an idea, behavior, or style that spreads by means of imitation from person to person within a culture and often carries symbolic meaning representing a particular phenomenon or theme.
An Internet meme or meme, is a cultural item that is spread via the Internet, often through social media platforms. The name is by the concept of memes proposed by Richard Dawkins in 1972. Internet memes can take various forms, such as images, videos, GIFs, and various other viral sensations.
- Wait at least 2 months before reposting
- No explicitly political content (about political figures, political events, elections and so on), !politicalmemes@lemmy.ca can be better place for that
- Use NSFW marking accordingly
Laittakaa meemejä tänne.
- Odota ainakin 2 kuukautta ennen meemin postaamista uudelleen
- Ei selkeän poliittista sisältöä (poliitikoista, poliittisista tapahtumista, vaaleista jne) parempi paikka esim. !politicalmemes@lemmy.ca
- Merkitse K18-sisältö tarpeen mukaan